📌 회귀분석의 종류
✔️ 단순 회귀 분석
- 특성의 개수가 1개이며 레이블과의 관계가 직선인 경우
✔️ 다중 회귀 분석
- 특성의 개수가 N개이며 레이블과의 관계가 선형인 경우(1차 함수)
✔️ 다항 회귀 분석
- 특성의 개수가 N개이며 레이블과의 관계가 비선형인 경우(1차 함수 이상)
✔️ 비선형 회귀 분석
- 회귀 식의 모양이 선형 관계로 이루어져 있지 않는 모델
📌 회귀 분석 성능 평가 척도
✔️ R-squared
- 실제 값의 분산 대비 예측 값의 분산 비율 (최고:1, 최악:음수)
- '설명력'이라고도 불림
✔️ Mean Absolute Error
- 실제 값과 예측 값의 차이를 절대값으로 변환하여 평균 계산
- 작을수록 좋지만 너무 작으면 과적합일 수 있음
✔️ Mean Squared Error
- 실제 값과 예측 값의 차이를 제곱해서 평균 계산
- 작을수록 좋지만 너무 작으면 과적합일 수 있음
- 이상치에 민감함
✔️ RMSE
- 모델간의 잔차 비교 가능
- 이상치에 덜 민감함 : 큰 오류값 차이에 대해 크게 패널티를 주기 때문
📌 Linear Regresson
- 레이블과 1개 이상의 특성과의 선형 상관관계를 모델링 하는 회귀 분석 기법
- 레이블과 연관 있는 특성이 존재하는 경우 관계 정량화 가능
- 단순 회귀 분석 : y = wx+b
- 다항 회귀 분석 : y = w1x1 + w2x2 + w3x3 + ... + wixi + b
-구현방법은 2가지 👉 a) 최소 제곱법 b) 경사 하강법
a) 최소 제곱법 (Ordinary Least Squared)
- 잔차(Residual, Error, y의 예측값과 실제 y값의 차이를 뜻함) 제곱의 합이 최소가 되도록 기울기(Weight)와 편향(Bias) 찾기
| [ 장점 ] | [ 단점 ] |
| 간단한 식 유도 가능 | 데이터가 많아질수록 계산량 증가 데이터에 이상치 있는 경우 성능 하락 |
👾 최소제곱법을 코딩으로 직접 실행해보자!
import numpy as np
# 이상치 미존재
x1 = np.array([10, 9, 3, 2])
y1 = np.array([90, 80, 50, 30])
# 이상치 존재
x2 = np.array([10, 9, 3, 2, 11])
y2 = np.array([90, 80, 50, 30,40])import matplotlib.pyplot as plt
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.scatter(x1, y1)
plt.title('Without Outlier')
plt.subplot(1, 2, 2)
plt.scatter(x2, y2)
plt.title('With Outlier')
plt.show()Matplotlib를 이용하여 원본 데이터를 시각화하게 되면 👇👇
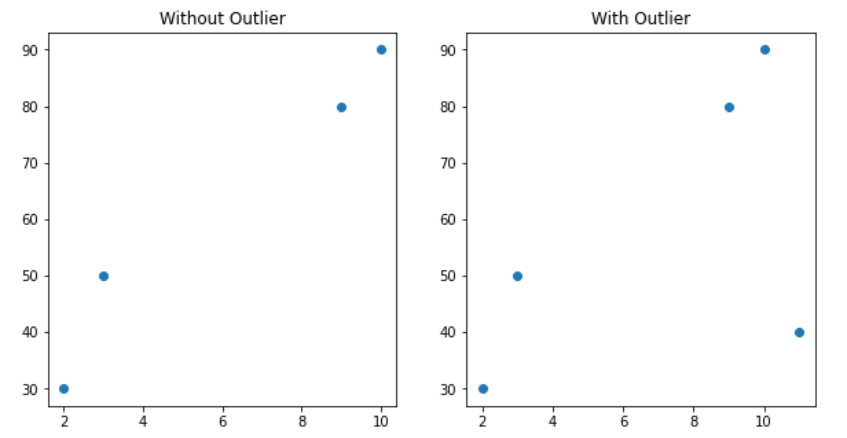
👉 여기서 이제 유도식을 직접 구현하여 입력되는 데이터에 대한 '잔차 제곱의 합'이 최소가 되는 가중치과 편향의 값을 계산 후 반환하는 함수 생성 👇
#최소 제곱법의 수식을 이용
def OLS(x, y):
w = np.sum((x-x.mean()) * (y-y.mean())) / np.sum((x-x.mean())**2)
b = y.mean() - w * x.mean()
return w, b
정의된 함수를 이용하여 가중치w와 편향b값을 계산해본다 👇
w1, b1 = OLS(x1, y1)
w1, b1
#output) (6.6, 22.900000000000006)
w2, b2 = OLS(x2, y2)
w2, b2
#output) (3.4285714285714284, 34.0)
계산된 가중치와 편향 값을 이용하여 예측 값을 계산 👇
x1_pred = x1 * w1 + b1
x2_pred = x2 * w2 + b2
이제 최소 제곱법을 이용한 결과를 시각화해보자 👇
plt.figure(figsize=(10, 5))
#subplot으로 박스 2개 만들기
plt.subplot(1, 2, 1)
plt.scatter(x1, y1, label='Sample')
plt.plot(x1, x1_pred, c='red', label=f'Y={w1:.2f}x+{b1:.2f}')
plt.legend()
plt.title('Without Outlier')
plt.subplot(1, 2, 2)
plt.scatter(x2, y2, label='Sample')
plt.plot(x2, x2_pred, c='red', label=f'Y={w2:.2f}x+{b2:.2f}')
plt.title('With Outlier')
plt.legend()
plt.show()
원본데이터를 시각화 한 것과 다름을 알 수 있음.. 보니까 빨간 선 하나가 추가 됐군!
With Outlier, 즉 이상치가 학습데이터에 포함되어 있는 경우 회귀선(빨간색 실선)과 데이터(파란 점) 사이의 잔차가 더 큰 것을 확인 가능
👾 위처럼 다 함수로 계산해서 어쩌구저쩌구..너무 귀찮다 그래서 최소 제곱법 모델을 그냥 가져오면 된다!
최소 제곱법 모델은 linear_model.LinearRegression으로 구현이 되어 있으며
✔️ coef_ : 가중치 값 조회 가능
✔️ Intercept_ : 편향 값 조회 가능
❗ 주의! scikit-learn의 ML 모델 특성은 '2차원 데이터'만 올 수 있기 때문에 1차원 데이터를 2차원 데이터로 reshape해준 후 가중치 및 편향 값 조회가 가능하다 ❗
from sklearn.linear_model import LinearRegression
model1 = LinearRegression().fit(x1.reshape(-1, 1), y1)
model1.coef_, model1.intercept_
#output) (array([6.6]), 22.899999999999984)
model2 = LinearRegression().fit(x2.reshape(-1, 1), y2)
model2.coef_, model2.intercept_
#output) (array([3.42857143]), 33.99999999999999)scikit-learn 을 이용하지 않고 직접 함수를 만들어 계산하여 진행한 것과 동일한 결과가 나온다
b) 경사하강법 (Gradient Descent)
- 가설에 의한 비용Cost를 최소화하는 직선을 구함
- 비용을 계산하기 위한 비용 함수가 필요하며 주로 평균 제곱 오차(MSE, Mean Square Error) 함수를 사용함
- 비용 함수를 미분하여 비용이 낮아지는 방향으로 가중치 값 변경하는 알고리즘
- 모델 단순화하기 위해 1개의 특성 이용
| [ 단점 ] |
| 모든 학습 데이터에 대해 반복적으로 비용 함수를 최소화하기 위한 값을 업데이트하기 때문에 수행 시간 오래 걸림 |
👾 경사하강법을 코딩으로 직접 실행해보자!
#경사 하강법
X = np.arange(50)
Y = (2 * X) + 10 * np.random.randn(50)
plt.plot(X, Y, 'b.')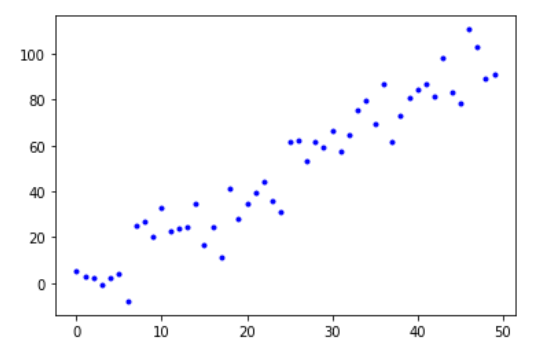
W값에 따른 비용 변화를 시각화해보면 👇
w_range = np.arange(0.1, 4.1, 0.1)
costs = []
#0.1, 4.1, 0.1 세개 range내에서 돌리기
for w in w_range:
h = w * X #가설 정의(모델 단순화하기 위해 편향 제외)
cost = 1 / 50 * np.sum( (h-Y) ** 2) #비용 함수 정의(평균 제곱 오차 함수 이용)
costs.append(cost)
plt.plot(w_range, costs, 'r.')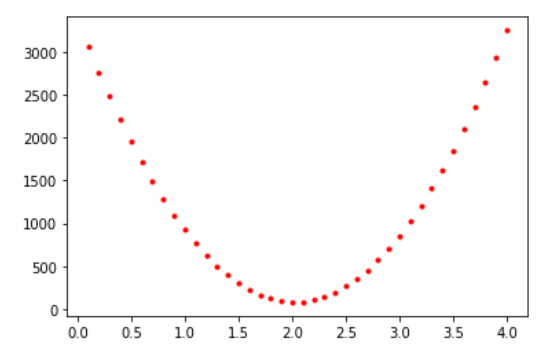
아... 머신러닝 어렵따...
'CDS' 카테고리의 다른 글
| Machine Learning [Coding Sample] (0) | 2021.11.16 |
|---|---|
| Machine Learning [Scaling] (0) | 2021.11.15 |
| Machine Learning [K-NN] (0) | 2021.11.15 |
| Machine Learning [Scikit-Learn] (0) | 2021.11.15 |
| Machine Learning Overview (0) | 2021.11.15 |